Opgave 5.1:
Uit hoeveel watermoleculen bestaat een echte waterdruppel eigenlijk? In figuur 5.1 zijn maar 12 watermoleculen getekend die samen een druppeltje moeten voorstellen. In een 3D tekening zouden het er een paar meer zijn, maar dan nog is het beslist geen reëel plaatje. Maak een berekende schatting van het aantal watermoleculen in een bolvormige waterdruppel met een diameter van 2 mm. Denk ook aan het getal van Avogadro. Gebruik hiervoor ook het gegeven uit figuur 5.2.
diameter waterdruppel: 2mm
diameter water molecuul: 2ɲm
Volume van een bol: 4/3 𝜋𝑟3
Volume van bol: 4/3 𝜋 2mm = 8.4 mm3
Volume watermolecuul: 4/3 𝜋 2ɲm = 8.4 mm3 = 8.4*10-21 mm3
Aantal watermoleculen per druppel = 8.4 mm3/8.4*10-21 mm3 = 1020
Opgave 5.2:
Leg uit waardoor de capillaire werking een grotere rol speelt naarmate de binnendiameter van de buis kleiner is. (Tip: de totale adhesiekracht is evenredig met het oppervlak van de vloeistofkolom tegen de buiswand en de totale zwaartekracht is evenredig met het volume van de vloeistofkolom.)
Het volume tot oppervlak verhouding zorgt ervoor dat het volume is afhankelijk van de hoeveelheid water, en de adhesie kracht hangt af van het oppervlakte van water dat contact maakt met de buiswand. En het volume die verandert tot de derde en en oppervlak tot de tweede dus neemt de adhesie kracht toe het water stijgt daardoor in nauwe cappilairen meer dan in wijde.
Opgave 5.3:
V) Bomen vervoeren water uit de grond via capillaire houtvaten naar de bladeren. Hoe hoog kan het water door de capillaire werking komen? Welke krachten spelen nog meer een rol in dit transport?
Niet zo hoog aangezien deze kracht niet genoeg doet zeker in verhouding met de grote van bomen. De krachten van osmose spelen ook een rol in dit transport.
Opgave 5.4:
Welk verband kun je ontdekken in de metingen van figuur 5.5? Maak dat verband op een duidelijke manier zichtbaar.
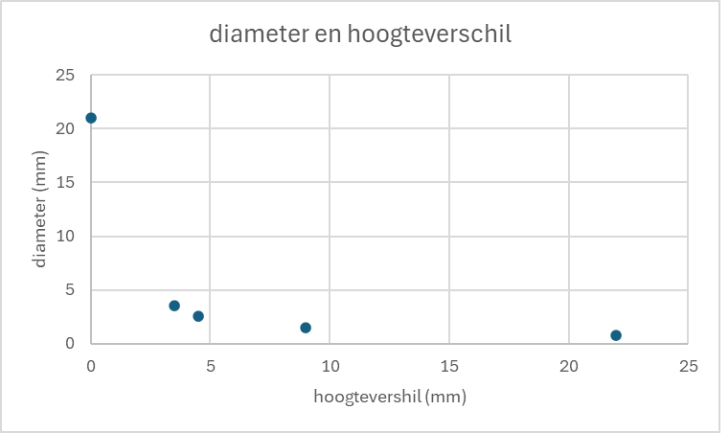
Er is een exponentieel verband tussen de adhesie kracht door de diameter van de buis en het hoogteverschil van de vloeistof in de buis. Dit verband is zichtbaar in de grafiek.
Opgave 5.5:
Leg uit of de cohesie van water groter of kleiner is dan de adhesie tussen olie en water.
De cohessie van water is groter dan de adhesie tussen olie en water omdat ze niet met elkaar mixen er vormen druppels van water in de olie dat niet in de olie wilt mixen.
Opgave 5.6:
Leg uit dat A.v (in figuur 5.12 bijvoorbeeld) het volume is dat per seconde door een doorsnede passeert.
v is de snelheid per seconde van het hoeveelheid vloeistof dat langs komt. Dit doe je dan * A de dwarsdoorsnede en dat is de hoeveelheid volume in een tijdseenheid dus m/s * m2 = m3 per seconden en m3 is volume.
Opgave 5.7:
De continuïteitsvergelijking hoeft niet te gelden voor een lang stuk van een rivier. Als bijvoorbeeld bij Zutphen een groter debiet van de IJssel gemeten wordt dan bij Zwolle, zal het waterpeil er bij Deventer (er tussen in) stijgen. Leg dat uit.
Er verdwijnt een deel van het water dit kan dan bij Deventer verzamelen en dan onstaat er een ophoping en dan stijgt er dus de waterpeil.
Opgave 5.8:
Beredeneer wat je moet doen om een laminaire stroming turbulent te maken: nauwer of wijder kanaaltje maken? Grotere stroomsnelheid instellen of juist kleinere?
Er komt turbulentie als je het breder maakt en ook als je het sneller laat stromen.
Hier hebben we de formule om het getal van Reynolds te berekenen dit getal geeft aan of er turbulentie is en als het groter is is er meer turbulentie Re = 2rρv/ɲ hier zien we dat als de r (straal van buis) en v (snelheid vloeistof) stijgt Re ook stijgt en er dus meer turbulentie is.
Opgave 5.9:
V Zoek in Binas op welke waarden voor ρ en η van water gelden bijkamertemperatuur. De straal van een rond kanaaltje in een chip is 0.030 mm. Maak een berekende schatting van de snelheid waarmee je water door dit kanaaltje kunt laten stromen zonder dat het turbulent wordt.
Dichtheid: 0,9982
Viscositeit: 0.001
V=Re∗η/2rρ =
